第9章排行榜服务——9.4 粗估排行榜的实现

John Yaml2025-05-022025-05-02

9.4 粗估排行榜的实现

由于担心大Key会对Redis的性能产生影响，所以你所在公司的Redis维护团队可能会强行限制在使用Redis时，单个ZSET的大小不能超过10000或其他阈值。这时确实没有办法使用一个ZSET实现百万人、千万人的排行榜，只能另辟蹊径。

我们先分析排行榜产品的特点。一个几千万人参与的排行榜，前几百名之后的用户会在乎他是第80001名还是第80002名吗？实际上，这些尾部用户最多会关心其大致排名是怎样的，当他有朝一日跻身彰显名次的头部位置时，才会对名次和与上一名的差距精打细算。

于是，我们就有了一个初步的想法：前N名用户使用ZSET精确排名，其他用户粗估排名。现在问题就可以聚焦到如何实现海量用户的粗估排名上了。

9.4.1 线段树

如果放宽对排名精度的要求，那么可以通过分段思想来释放排行榜所需的大量存储空间：把积分按固定范围分成多个等长的分段，每个分段都保存当前积分处于此分段的用户数量，如图9-3所示。

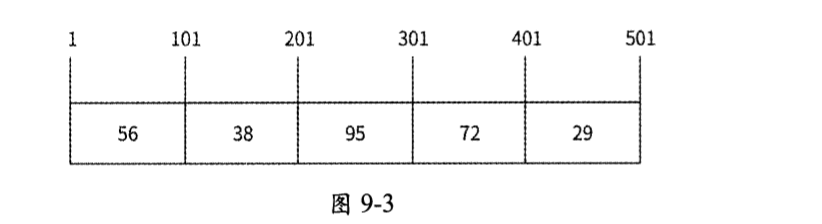
请看图9-3，假设排行榜积分上限是500，现在将排行榜分为5个分段，其中第1个分段存储积分在[1, 100]范围的用户数量，第2个分段存储积分在[101, 200]范围的用户数量。假设某用户目前积分为150，分段粗估此用户排名的过程如下。

从最高分段开始向前遍历，直到找到此用户的积分所在的分段[101, 200]。
在遍历过程中，将高分段人数累加求和，即95 + 72 + 29 = 196，这是积分大于200的用户总数。
在[101, 200]分段中计算此用户的预估排名。因为假设分段中所有的用户积分都是均匀分布的，所以积分为150的这个用户在此分段中的排名为(200 - 150) × 38 ÷ 100 = 19。
更高分段中的人数总和与此用户在[101, 200]范围的排名相加，得到其最终排名为196 + 19 = 215。

可以看到，所谓的粗估排名就体现为假设每个分段中的用户积分都是均匀分布的，所以分段的长度直接决定了排名的精度，长度越短，精度越高，但是分段数目也越多。

如果分段数目较多，那么从最高分段遍历就不太合适了，这个时间复杂度为O(N)的操作会降低查询效率。在这个场景中适合的数据结构是线段树，它以二叉树的形式维护多个分段，并可以在O(logN)时间内实现数据修改、区间查询等操作。

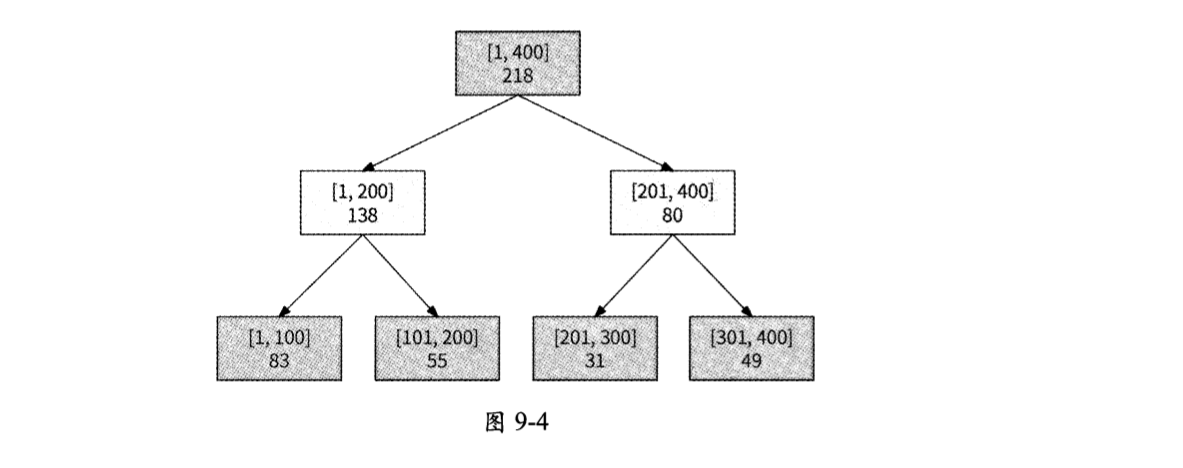
线段树的根节点表示的数据区间覆盖了整个数据范围，每个节点表示的数据区间都是它的子节点所表示的数据区间的合集。对于一个积分上限是400、有4个分段的排行榜，使用线段树构建的结构如图9-4所示。

其中：

每个分段均为叶节点，作为线段树的第3层节点。
每两个相邻分段被合并为更大的数据区间，作为线段树的第2层节点。每个数据区间的长度都为200，区间内的数据数量是分段数据数量的总和。
根节点覆盖整个数据范围，即[1, 400]，区间内的数据数量表示全部数据。

当给定排行榜的积分上限和值为2的幂次方的分段数目时，使用Go语言实现的创建线段树的代码如下：

1	// 线段树节点结构

9.4.2 粗估排名的实现

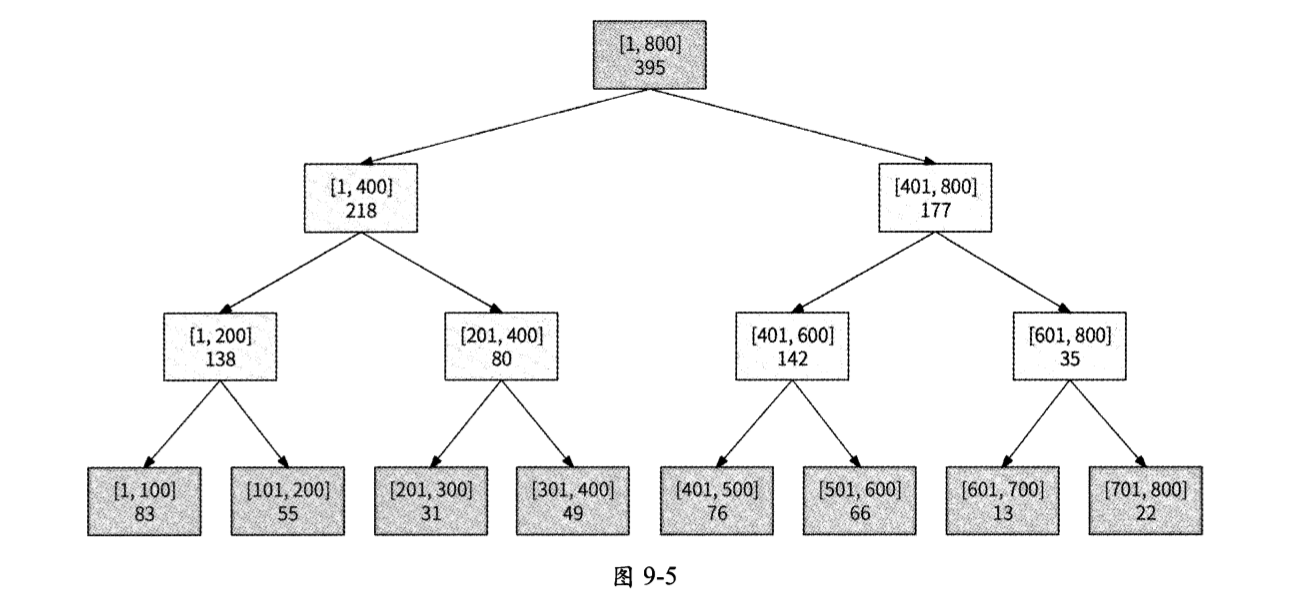
使用线段树实现排行榜排名，需要支持的两个操作分别是查询排名和更新排名。我们以图9-5中使用线段树构建的排行榜为例。

在查询用户排名时，由于线段树并未存储用户的真实积分，所以需要传入用户的最新积分，然后从线段树的根节点开始向下遍历。假设某用户积分为220，查询其排名的过程如下：

根节点发现220在左子节点[1, 400]范围内，于是遍历左子节点。
[1, 400]节点发现220在右子节点[201, 400]范围内，于是遍历右子节点。
[201, 400]节点发现220在左子节点[201, 300]范围内，于是继续遍历左子节点。
[201, 300]是叶节点，即最终的分段，此时计算出该用户在此分段的预估排名为(300 - 220) × 31 ÷ 100 ≈ 25。
在从根节点开始的完整遍历过程中，如果某节点选择继续遍历左子节点，则说明右子节点代表的数据区间大于220，此时需要累加右子节点的用户数量，最终得到[201, 300]分段之外的大于220的用户总数。对于本例来说，就是[401, 800]和[301, 400]这两个节点的累加和，即177 + 49 = 226。
将全部大于220的用户数量加和，得到此用户的最终排名为226 + 25 = 251。

整个查询排名过程的时间复杂度为O(logN)，对应的Go语言代码如下：

1	// 在线段树中查询某积分对应的排名

在更新用户排名时，需要使用更新前的积分score1和更新后的最新积分score2。

从线段树的根节点开始遍历score1，在遍历过程中经过的所有节点都将用户数量减1。
从线段树的根节点开始遍历score2，在遍历过程中经过的所有节点都将用户数量加1。

更新用户排名由删除（先执行）和插入（后执行）两个操作组成，时间复杂度也为O(logN)，其Go语言代码如下：

1	// 遍历线段树，并修改遍历过的节点

在解释了查询排名和更新排名的流程后，我们再说明一个重要的问题。线段树方案把区间内的用户数量存储在线段树的各节点上，但是线段树是内存型数据结构，而内存无法被多个服务实例共享，所以这种线段树实现方式要求排行榜服务只能有一个服务实例，这无论是从服务的高可用性、高性能还是可扩展性方面来讲都是难以接受的。

我们再来分析一下使用线段树实现排行榜的特点。线段树的结构是固定不变的，只不过每个节点的用户数量在变化。那么，我们是否可以只在内存中保存线段树结构，而将每个节点的用户数量交给某个存储系统来保存？

答案是肯定的，使用Redis的Hash结构就可以轻松实现这个目的。一个Hash对象表示一棵线段树，线段树的每个节点都用Field字段表示，对应的Value存储节点的用户数量。所以，上例的线段树结构在Redis中会被保存为图9-6所示的形式。

这样一来，排行榜服务可以有任意多个服务实例。如图9-7所示，每个服务实例都在本地调用BuildSegmentTree函数创建线段树结构（由于线段树结构是固定的，所以必然每个服务实例都创建了一模一样的线段树），而线段树每个节点的具体分数通过Redis Hash来读/写。

在查询用户排名时，服务实例使用本地内存中的线段树获取此次需要查询的节点的用户数量，然后向Redis发送HMGET命令获取各个节点数据。
在更新用户排名时，服务实例使用线段树获取删除score1要更新的节点，以及新增score2要更新的节点，然后借助Redis Lua脚本对这些节点执行HINCRBY命令来更新用户数量。

例如：查询积分为220的用户排名，需要从Redis Hash中获取Field为201-300、301-400、401-800的Value；将用户积分从220更新到750，需要对Field为1-800、1-400、201-400和201-300的Value减1，对Field为1-800、401-800、601-800和701-800的Value加1。

至此，基于线段树的排行榜实现已经非常清晰了。关键的Go语言代码如下：

1	// 获取线段树中需要更新的节点，即遍历过的节点

线段树方案仅使用一个成员极少的Hash对象就实现了排行榜粗估排名，而无视参与者人数，节约了大量存储空间，可谓是“四两拨千斤”。不过，线段树并不存储每个用户的具体分数，所以它注定存在如下一些缺点。

排名不精确：线段树假设一个分段内的用户积分是均匀分布的，所以为精确排名带来了不确定性（这是我们已知的缺点）。
不支持获取排名列表：线段树只存储每个分段的用户数量，它可以高效支持已知积分用户的粗估排名，但是并不支持获取排行榜有哪些用户参与，以及每个用户的积分。

如果单纯使用线段树方案，则适合全民参与的，且在其他系统中维护积分的场景。比如QQ等级，由用户登录时间累积得到的太阳、月亮、星星的数量会由专门的等级服务维。如果要对QQ的全部用户按照等级排名，并为每个用户展示其排名，那么就很适合使用线段树方案。

总结

如果确实没有办法使用一个ZSET实现百万人、千万人的排行榜，那该怎么办呢？

前N名用户使用ZSET精确排名，其他用户粗估排名。

如果放宽对排名精度的要求，那么如何通过分段思想来释放排行榜所需的大量存储空间？

把积分按固定范围分成多个等长的分段，每个分段都保存当前积分处于此分段的用户数量。

如何理解粗估排名？

所谓的粗估排名就体现为假设每个分段中的用户积分都是均匀分布的，所以分段的长度直接决定了排名的精度，长度越短，精度越高，但是分段数目也越多。

为什么使用线段树来做粗估排名？

如果分段数目较多，那么从最高分段遍历就不太合适了，这个时间复杂度为O(N)的操作会降低查询效率。
在这个场景中适合的数据结构是线段树，它以二叉树的形式维护多个分段，并可以在O(logN)时间内实现数据修改、区间查询等操作。

为什么线段树实现方式要求排行榜服务只能有一个服务实例？

线段树方案把区间内的用户数量存储在线段树的各节点上，但是线段树是内存型数据结构，而内存无法被多个服务实例共享。
所以这种线段树实现方式要求排行榜服务只能有一个服务实例，这无论是从服务的高可用性、高性能还是可扩展性方面来讲都是难以接受的。

如何解决呢？

我们再来分析一下使用线段树实现排行榜的特点。线段树的结构是固定不变的，只不过每个节点的用户数量在变化。那么，我们是否可以只在内存中保存线段树结构，而将每个节点的用户数量交给某个存储系统来保存？
答案是肯定的，使用Redis的Hash结构就可以轻松实现这个目的。一个Hash对象表示一棵线段树，线段树的每个节点都用Field字段表示，对应的Value存储节点的用户数量。

线段树方案的缺点？

排名不精确：线段树假设一个分段内的用户积分是均匀分布的，所以为精确排名带来了不确定性（这是我们已知的缺点）。
不支持获取排名列表：线段树只存储每个分段的用户数量，它可以高效支持已知积分用户的粗估排名，但是并不支持获取排行榜有哪些用户参与，以及每个用户的积分。